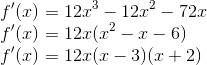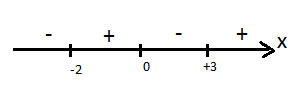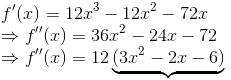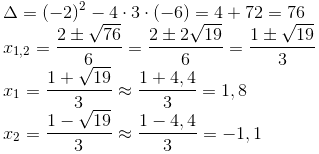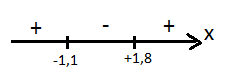Mat 2016 – Questão 6

0-Falso

Para ser crescente, deve ter primeira derivada positiva:

Pela fórmula acima, vemos que a derivada troca de sinal quando x=-2, 0 e 3. Quando x→+∞, f’→+∞ também, ou seja, f’ é positiva. Considerando as trocas de sinais em -2, 0 e 3, veja os sinais de f’:

Logo, f não é crescente em todo intervalo [0; +∞[, pois é decrescente em [0;3].

1-Falso

Como vimos no item anterior, a derivada de f é nula em x=-2, 0 e 3.

2-Verdadeiro

Para ser côncava, a segunda derivada deve ser negativa:

Para verificar o sinal de f”, vamos encontrar as raízes de 3x²-2x-6:

Quando fazemos aproximações como no cálculo da raiz acima, sempre é bom ter em mente o tamanho do erro que podemos estar cometendo para ver se mudaria algo no resultado final. No caso, como aproximamos na primeira casa decimal, o erro máximo de x_1,2 é:

O que não nos vai causar problema já que x₂ continuará menor que -1 mesmo considerando esse erro máximo.

Quando x→+∞, f”→+∞, ou seja, f” é positiva. Considerando que troca de sinal em x₁ e x₂:

Assim, a f” é negativa entre -1 e 1, o que torna f côncava nesse intervalo.

3-Falso (gabarito Anpec: Verdadeiro)

Para uma função ter inversa, ela deve ser bijetora: injetora e sobrejetora.

No intervalo de 0 a 3, a função f é estritamente decrescente, já que f’ é positiva (ver figura 1).

Toda função estritamente crescente é injetora, pois, uma vez que a função sempre cresce, não há dois valores de x que atinge o mesmo valor depois que aplicamos f.

O problema aqui é verificar se a função é sobrejetora no intervalo. Para verificar isso, o contra-domínio deve estar definido.

É possível estabelecer um contra-domínio de forma que a função seja sobrejetora. Se fizermos isso, a função será bijetora e, portanto, inversível.

No entanto, não podemos dizer que ela é inversível para qualquer contra-domínio.

Dessa forma, diria que a questão é falsa. Contudo, esse é o tipo de questão que vale a pena deixar em branco, já que pode parecer muita picuinha considerá-la falsa por um problema de falta de dado (o contra-domínio) no enunciado.

4-Falso

Quando x→-∞, a parcela 3x⁴ fica tão grande em relação às demais, que as torna desprezíveis. Logo, como 3x⁴→ +∞ quando x→-∞, f(x) também tende a +∞.