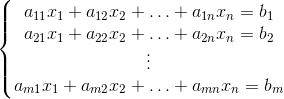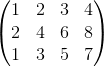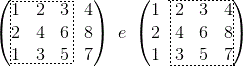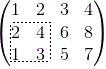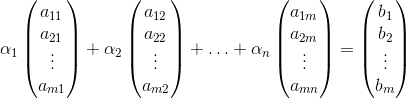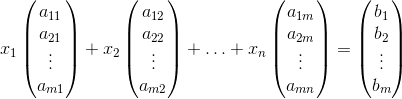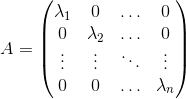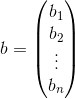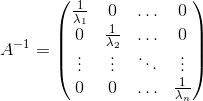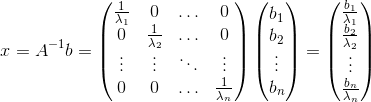Preliminares
Apenas para visualizar melhor o problema, estamos falando do seguinte sistema:
Que é um sistema com n variáveis e m equações.
0-Falso
Se o determinante for nulo, ocorre uma de duas situações: ou o sistema não tem solução ou o sistema tem infinitas soluções.
Logo, não podemos afirmar com certeza que o sistema não terá soluções.
1-Falso
Descobrimos o posto de uma matriz encontrando a maior submatriz quadrada que tem determinante diferente de zero. Por exemplo, seja a matriz abaixo:
Como ela é 3×4, a maior submatriz quadrada é 3×3, que são as submatrizes abaixo:
No entanto, essas submatrizes possuem determinante igual a zero, já que a segunda linha é exatamente o dobro da primeira. Assim, não há submatriz 3×3 com determinante diferente de zero.
Vamos analisar as submatrizes 2×2. Veja a submatriz destacada:
Ela tem determinante igual a 2. Como ela é 2×2, dizemos que o posto da matriz original é 2.
Voltando para a questão: o que seria uma matriz de posto máximo?
O máximo posto que uma matriz m x n pode ter ocorre quando sua maior submatriz quadrada tem determinante diferente de zero. Temos duas situações que podem ocorrer:
(1) m<n: a maior submatriz quadrada seria m x m e teria determinante diferente de zero, sendo a matriz original de posto m.
(2) m≥n: a maior submatriz quadrada seria n x n e teria determinante diferente de zero, sendo a matriz original de posto n.
Vamos iniciar pela situação (1):
Se m<n, há mais variáveis do que equações no sistema. Quando isso ocorre, há infinitas soluções no sistema (precisamos de m variáveis para resolver um sistema de m equações linearmente independentes, então as outras (n-m) variáveis poderiam ter qualquer valor, gerando infinitas soluções). Logo, a afirmativa é falsa.
Como já vimos que a sentença é falsa, não precisamos analisar a situação 2. Apenas para constar, é um caso em que há apenas uma solução ou nenhuma. Logo, olhando somente para esta situação, a afirmativa também seria falsa.
2-Falso
Essa é a situação 1 do item anterior.
3- Verdadeiro
Se o vetor b é combinação linear das colunas de A, quer dizer que existem “pesos” α1, α2, α3,…, αn tal que:
Veja que, de fato, o sistema pode ser reescrito como:
Comparando as duas fórmulas acima, fica claro que existe ao menos a seguinte solução para o sistema:
Em que os xi’s são os pesos das colunas de A na formação de b.
4- Verdadeiro
Seja A a seguinte matriz diagonal :
E b o vetor:
O sistema, na forma matricial, é o seguinte:
Isolando x, temos:
Como a matriz A é diagonal, fica fácil calcular sua inversa:
Assim:
Logo, a solução é xi=bi/λi, i=1, 2,…, n.
A média geométrica desses n valores é:
Note que:
Logo, de (*):
Assim, podemos dizer que a média geométrica dos xi’s é inversamente proporcional a ![]() .
.