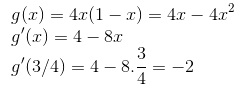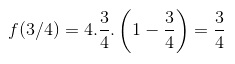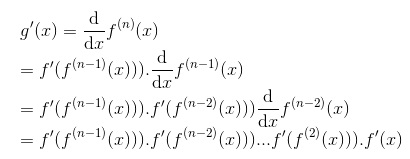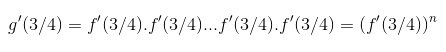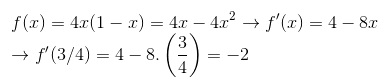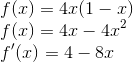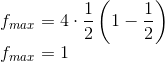Mat 2016 – Questão 3

0-Verdadeiro

Para f ser uma bijetora, ela deve ser injetora e sobrejetora.

Vamos calcular a primeira derivada:

Como x² sempre é não negativo:

Já que a derivada de f sempre é positiva, f é estritamente crescente. Se f é estritamente crescente, quer dizer que não temos dois valores diferentes de x que chegam ao mesmo valor depois que aplicamos f neles (já que se a<b, então f(a)<f(b)). Dessa forma, f é injetora.

Para verificar que f é sobrejetora, basta ver que f→-∞ quando x→-∞ e f→+∞ quando x→+∞. Como f é contínua, f “passa” por todos os valores, de -∞ a +∞, e logo a imagem de f é igual ao seu contra-domínio, o conjunto dos números reais. Dessa forma, f é sobrejetora.

Como f é injetora e sobrejetora, f é bijetora.

1-Falso

1º modo

Ao fazer a prova da Anpec, nunca podemos esquecer que ninguém vai ver nossa solução. Logo, se não estamos resolvendo do jeito mais rigoroso possível, não há problema, o que importa é a resposta. Entre resolver direito e resolver rápido, é melhor escolher a segunda opção.

Numa questão desse tipo, é sempre bom checar casos particulares fáceis para ver se a alternativa é falsa. Se não funciona para um caso particular, quer dizer que não podemos generalizar e a alternativa não é verdadeira.

Nessa questão em específico, verifiquemos o caso em que n=1, g(x)=f(x):

Para o item ser verdadeiro, quando n=1, g’(3/4) deveria ser igual a (3/4)¹=3/4. Dessa forma, o item é falso.

2º modo

Vamos para o jeito mais “correto”.

Primeiro verifique que x=3/4 não foi escolhido à toa:

Ou seja, chegamos ao próprio 3/4 quando aplicamos f em 3/4. Dessa forma, mesmo aplicando f várias vezes ao ponto 3/4, nunca vamos deixar de chegar no 3/4. Por exemplo:

Como g(x)=f⁽ⁿ⁾(x), vamos calcular a derivada de g(x) utilizando a regra da cadeia várias vezes:

Substituindo x=3/4:

Como vimos anteriormente, qualquer composição de funções f aplicada a x=3/4 chega em 3/4 (f^(k)(3/4)=3/4 para todo k natural):

Agora vamos calcular f’(3/4):

Substituindo em g’(3/4):

2-Falso

Para uma função f ser sobrejetora em R, seu conjunto imagem deve ser igual ao conjunto dos números reais, ou seja, para todo valor real, existe um x tal que f(x) seja igual a esse valor (f “leva” pelo menos um x para qualquer valor real).

A função sobrejetora mais simples que me vem à cabeça é f(x)=x (quando x varia percorrendo todos os números reais, f(x) também percorre todos os números reais).

O produto de f por f, que é um produto de funções sobrejetoras, é igual a f(x). f(x)=x², que não é sobrejetora, uma vez que x² não atinge os números reais negativos.

3-Falso

Para uma função f ser injetora não pode ter dois ou mais valores de x que atingem o mesmo valor depois de aplicar f, ou seja, se a≠b, então f(a)≠f(b).

Nesse caso, o domínio é o conjunto dos candidatos. Como pode haver mais de um candidato com a mesma nota, essa função que associa candidatos a notas não é necessariamente injetora.

Por exemplo, se João e José tiraram ambos a nota 7,5, essa função iria associar tanto João quanto José a nota 7,5, o que implica numa função não sobrejetora.

4-Verdadeiro

Primeiro, note que f não atinge valores negativos quando x está entre 0 e 1. Dessa forma, seu ponto de mínimo ocorre quando x=0 ou 1, de forma que a função atinge o valor 0.

Agora vamos encontrar agora o ponto de máximo de f. Para isso, temos que encontrar a primeira derivada:

Apenas para ter certeza que é ponto de máximo, note que a segunda derivada é negativa.

O ponto de máximo ocorre somente quando a derivada é igual a 0, assim:

Encontramos o valor de x que maximiza f. Vamos substituir esse x na função para encontrar o maior f:

Assim, f(x) é limitada entre 0 (valor mínimo que atinge) e 1 (valor máximo que atinge). Ou seja, f atinge os mesmo valores que x atinge, e podemos dizer que Domínio de f=Imagem de f=[0,1].

Agora vamos analisar a função f(f(x)):

Como o f(x) que está no argumento da função (o de dentro) varia entre 0 e 1 (assim como x), f(f(x)) também atinge seu valor máximo em f(f(x))=1, e quando f(x)=1/2 (lembra que f(x) chegava ao máximo quando x=1/2?).

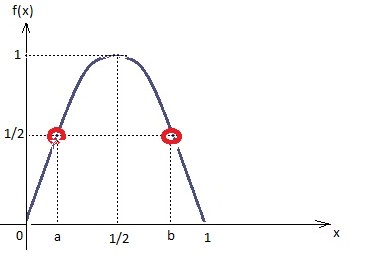
Só que f(x)=1/2 ocorre em dois pontos, uma vez quando x está entre 0 e 1/2 e outra quando está entre 1/2 e 1:

Da mesma forma, f(f(f(x))) também atinge seu máximo em f(f(f(x)))=1, e isso ocorre quando f(f(x))=1/2.

Mas f(f(x))=1/2 ocorre para dois valores de f(x), uma vez quando f(x) é menor que 1/2 e mais uma quando f(x) é maior do que 1/2.

Seja f(x)=a, a<1/2, e f(x)=b, b>1/2, de tal forma que f(f(a))=f(f(b))=1/2.

Como f forma uma parábola, existem dois valores de x que fazem f(x)=a e mais dois valores de x que fazem f(x)=b. Completando, dessa forma, quatro soluções.

Sei que ficou bem confuso, então tentar explicar de novo:

-O valor máximo de f é 1

–f atinge 1 quando seu argumento é 1/2, ou seja, f(alguma coisa)=1 quando alguma coisa=1/2

-Assim, f(f(x)) atinge 1 quando f(x)=1/2

–f(x) atinge 1/2 em dois valores de x, vamos chamar de a e b (conforme último gráfico)

-f(f(f(x))) atinge 1 quando f(f(x))=1/2, e isso ocorre quando f(x)=a e quando f(x)=b

-f(x)=a em dois pontos e f(x)=b em outros dois pontos, totalizando quatro valores de x em que f(f(f(x)))=1, todos pontos de máximo