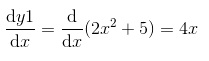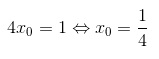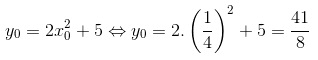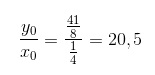Questão 2
Resolução
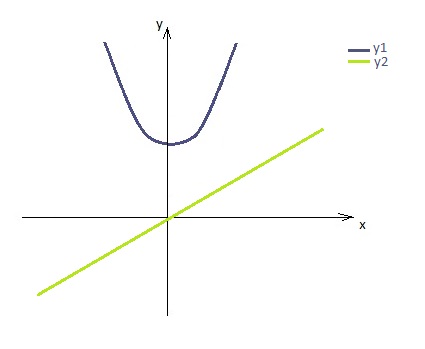
Seja y1=2x2 +5 e y2=x. Observe um esboço das duas curvas:
Qual ponto da parábola está mais próximo da reta?
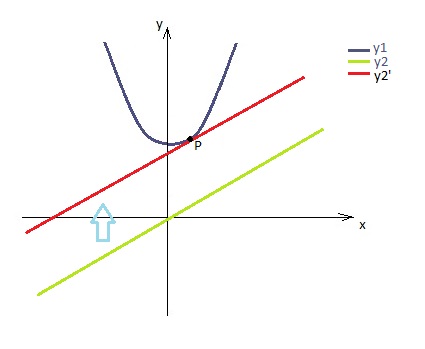
Como descobrir o ponto de y1 que está mais próximo de y2? Difícil… para facilitar, vamos deslocar a reta y2 até ela tocar na curva y1:
Encontramos y2’: uma reta paralela à y2 e tangente à parábola.
Se a pergunta fosse qual o ponto da parábola mais próximo dessa reta y2’, a resposta seria fácil: o ponto de intersecção entre as duas curvas, P.
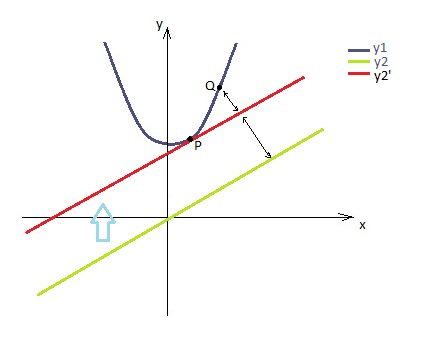
Bom, mas agora ficou mais fácil responder a pergunta original: o ponto de y1 mais próximo de y2 é o mesmo ponto P. Por quê?
Seja Q um ponto qualquer da parábola. A distância entre Q e a reta y2 é igual à distância entre Q e y2’ mais a distância de y2’ e y2:
Como a distância entre y2’ e y2 é igual para qualquer ponto (já que são retas paralelas), o ponto de y1 que tem a menor distância para y2 é aquele que tem a menor distância para y2’, ou seja, P, cuja distância para y2’ é zero:
Menor dist(Q,y2) quanto menor dist(Q,y2’). Se Q for o ponto P, minimizamos dist(Q,y2’) para zero.
Determinando o ponto P=(x0,y0):
(1) A reta y2’ é uma reta paralela à y2, dessa forma, essas retas possuem o mesmo coeficiente angular: 1 (já que y=1x para y2).
(2) Além disso, a reta y2’ é a reta tangente à parábola no ponto P, então seu coeficiente angular deve ser igual à derivada de y1 em relação a x nesse ponto:
De (1) e (2):
Como P pertence à parábola, para encontrarmos y0 basta substituirmos x0 na fórmula da parábola:
Para obtermos a resposta final, basta dividir y0 por x0 e pegar a parte inteira:
Resposta: 20