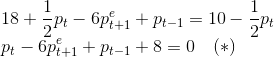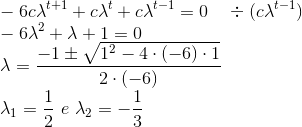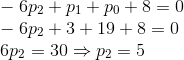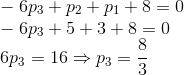Mat 2016 – Questão 11

Preliminares

Considerando que, no equilíbrio, a oferta é igual à demanda:

0-Verdadeiro

Sob expectativas racionais, substituímos p^e_t+1= p_t+1 em (*):

Se um preço é estacionário, uma vez atingido, ele permanece igual em todos os demais instantes.

Assim, para descobrir o preço estacionário, vamos substituir os preços de todos os instantes da igualdade acima por uma única variável p:

Logo 2 é um preço estacionário.

1-Falso

Temos que resolver a equação a diferenças de (**).

Primeiro, vamos considerar a parte homogênea da equação:

Como é uma equação linear homogênea, a solução é da seguinte forma:

Substituindo na equação homogênea:

Encontramos dois valores para λ, assim a solução da equação homogênea é:

Para a solução final, temos que adicionar a solução particular. Como visto no item 0, a solução particular p_p=2 satisfaz a equação. Assim, temos:

Não vamos nos preocupar com as constantes c₁ e c₂ por enquanto. Importante para este item é perceber que, quando t aumenta, p_t se aproxima de 2, uma vez que os λ’s tem módulo menor que 1. Logo, a dinâmica de preços converge.

2-Verdadeiro

De (**):

E:

3- Falso

Substituindo p^e_t+1= p_t-1 em (*):

Novamente, para verificar o preço estacionário devemos substituir os preços em qualquer instante de tempo por um preço único p:

O preço estacionário continua sendo p=2.

4-Verdadeiro

A equação homogênea de (***) é:

Novamente, a solução da equação homogênea tem a seguinte forma:

Substituindo essa solução na equação homogênea:

Como visto no item anterior, note que p=2 é a solução particular. Assim, a solução de (***) é:

Note que o preço tende a explodir, já que 5^t cresce infinitamente a medida que t aumenta.