
Introdução
Esse artigo, com relação aos demais que temos no site, pode ser considerado bastante técnico. Para entender ele, será necessário conhecimento de probabilidade, mas nada além do que a Anpec exige. Assim, para você que está preparado para a prova de estatística, espero que, além de achar uma aplicação interessante da matéria, também consiga revisar um pouco para a prova!
Já adianto que a aplicação estrita das ideias que serão expostas será muito complicada de ser feita na prática, simplesmente porque alguns dos parâmetros que vamos utilizar não são observáveis na realidade.
De qualquer forma, o que espero é fazer você ao menos se questionar do que vale a pena fazer com relação aos itens que você não tem certeza da resposta.
Uma coisa eu posso dizer com convicção: você não precisa estar 100% certo da resposta para decidir responder uma questão. O que não significa que é para você sair respondendo todos os itens sem critério algum!
O Problema
Suponha que Joãozinho fez a prova da Anpec. Após responder todas as perguntas cujas respostas ele de fato sabia, restaram 10 itens que ele tinha uma ideia da resposta. Considere que, para cada um desses itens, ele tem 60% de chance de acertar se ele escolher responder.
Lembre-se de que, como só tem duas respostas possíveis, verdadeiro ou falso, chutar a resposta de forma completamente aleatória te dá uma probabilidade de 50% de acerto (você poderia jogar uma moeda e responder “Verdadeiro” se der cara ou “Falso” se der coroa, por exemplo). Enfim, esse não é o caso de Joãozinho, ele tem ao menos um pouco de noção da resposta sobre esses 10 itens, o que lhe dá uma probabilidade de 60% de acerto para cada item respondido.
Considere dois cenários: no primeiro, Joãozinho não responde nenhum desses 10 itens dos quais ele não tem certeza da resposta; no segundo, ele responde todos. A pergunta é: qual dos cenários Joãozinho deve escolher? É melhor “chutar” os 10 itens ou não responder nenhum?
Se a Anpec não punisse um item errado, dando nota negativa para ele, certamente sempre valeria a pena responder todas as perguntas da prova. Mas esse não é o caso, então vamos analisar esse problema com mais cuidado.
Modelando o Problema com Estatística
Joãozinho tem 10 itens cujas respostas não tem certeza. Vamos chamar esses itens de 1, 2, …, 10. Além disso, considere que X1 é uma variável aleatória igual a 1, se for o caso em que Joãozinho acertaria o item 1 se o respondesse, e 0, caso contrário.
De forma análoga, considere as variáveis aleatórias X2, X3, …, X10 tal que Xi=1, se Joãozinho fosse acertar o item i se o respondesse, e Xi=0, caso contrário. A gente vai considerar que essas variáveis são independentes.
Note que cada um dos Xi’s tem uma distribuição de Bernoulli, uma vez que podem assumir somente os valores 0 ou 1. Como Joãozinho teria 60% de chance de acertar o item caso o respondesse, o parâmetro dessa distribuição de Bernoulli é p=0,60.
Considere a variável aleatória X= X1+ X2+…+ X10, que representa o total de acertos que Joãozinho teria caso decidisse responder os 10 itens. Como X é uma soma de 10 variáveis independentes com distribuição de Bernoulli de parâmetro p=0,60, sabemos que X tem uma distribuição binomial com parâmetros n=10 e p=0,60.
Valor Esperado vs Variância
O valor esperado da quantidade de acertos X, com distribuição binomial com parâmetros n=10 e p=0,60, é dado por:
E[X]=np=10.0,6=6
Em termos de valor esperado, faz bastante sentido Joãozinho decidir responder os 10 itens, já que o valor esperado da quantidade de acertos, 6, é maior do que o valor esperado da quantidade de erros, 10-6=4.
Por outro lado, note que a variância de X é:
Var[X]=np(1-p)=10.0,6.(1-0,6)=2,4
E, para relembrar outra medida de dispersão, o desvio padrão de X é:
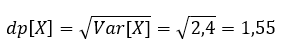
A variância/desvio padrão dos acertos de Joãozinho é que nos faz ter dúvidas se vale a pena responder os 10 itens: responder esses itens trará incerteza sobre sua nota, o que pode fazer com que a quantidade de erros seja maior do que a quantidade de acertos, por mais que o valor esperado da quantidade de erros, 4, seja menor do que o valor esperado da quantidade de acertos, 6.
Distribuição da Quantidade de Acertos
Então responder os 10 itens é bom em termos de valor esperado, mas ruim por aumentar a variabilidade na nota de Joãozinho, podendo inclusive diminuí-la significativamente. Para entender a chance disso ocorrer, precisamos ir atrás da distribuição da quantidade de acertos.
Sabendo a função de probabilidade de uma variável com distribuição binomial de parâmetros n=10 e p=0,60, podemos ver a probabilidade da quantidade de acertos X assumir cada valor entre 0 e 10:
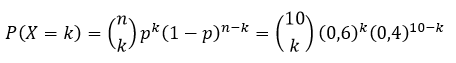
Fazendo as contas para cada k entre 0 e 10, temos a distribuição representada abaixo:
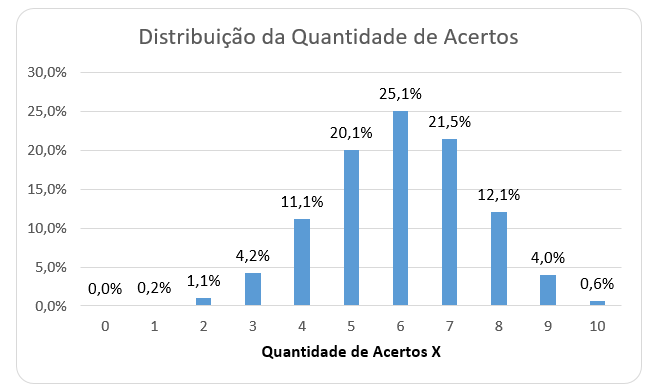
Com isso, somando os valores das barrinhas com X menor do que 5, já podemos calcular a probabilidade de, respondendo os 10 itens, a quantidade de acertos ser menor do que a quantidade de erros, fazendo com que Joãozinho tenha uma nota negativa nesses itens:

Assim como a probabilidade de, respondendo os 10 itens, o impacto na nota ser positivo:
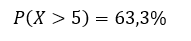
Note que as duas probabilidades não somam 100% pois há uma chance de X ser igual a 5, o que não impactaria a nota.
Outra Variável Aleatória
Até agora temos trabalhado com a variável aleatória X, que representa a quantidade de acertos dentro dos 10 itens respondidos.
No entanto, a variável aleatória que de fato importa é a nota que Joãozinho tiraria com os 10 itens respondidos. Chamemos essa variável aleatória de N.
Vamos considerar que cada item correto vale 0,2 e cada item incorreto vale -0,2, assim como ocorre com a maior parte dos itens da Anpec (tirando questões que tem itens anulados). Assim, N pode ser calculado como uma função da variável X:
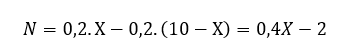
O que nos permite calcular valor esperado e desvio padrão de N:
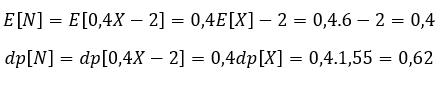
E, mais importantemente, a distribuição de N:
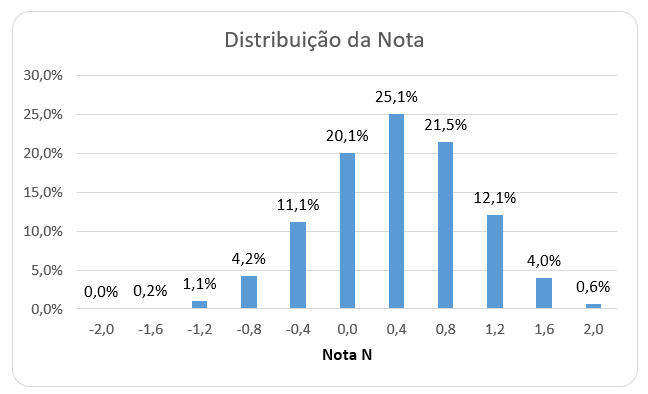
Note que é praticamente a mesma distribuição de X, mudando apenas o eixo horizontal. Isso ocorre porque cada valor X está associado a somente um valor de N, e vice-versa.
Interessante que, com essa distribuição, podemos fazer perguntas um pouco diferentes. Por exemplo, respondendo os 10 itens:
- Qual a probabilidade de perder mais de 1 ponto na nota final?
- Seria P(N<-1)=1,3%.
- Qual a probabilidade de ganhar mais de 1 ponto na nota final?
- Seria P(N>1)=16,7%.
Assim, ao decidir por responder os 10 itens, a chance de ter um impacto negativo grande na nota é bastante baixa; enquanto a chance de ter um impacto positivo relevante é significativa.
Outros Cenários
Até agora trabalhamos com n=10 itens, com chance de p=60% de acerto para cada um deles caso respondido. Fizemos isso mais para explicar as contas de estatística por trás da análise. Agora vamos aumentar a quantidade de “chutes” e ver o impacto disso na nota.
Quando aumentamos a quantidade de itens respondidos, a média da quantidade de acertos aumenta, mas também a variância. Ou seja, a distribuição dos acertos fica mais deslocada para a direita, além de ficar mais larga.
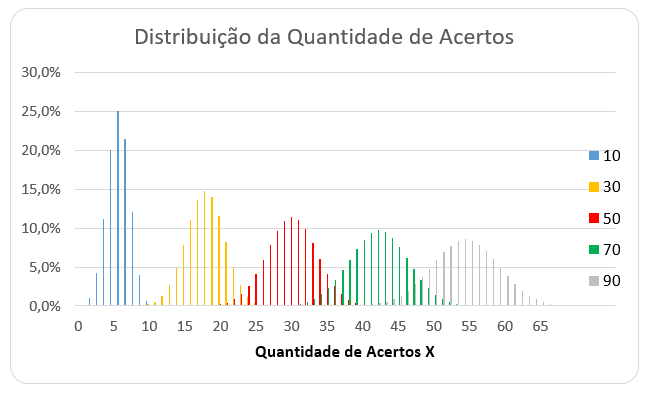
É claro que, quanto mais itens respondidos, mais fácil será ter mais acertos. No entanto, também será mais fácil ter mais erros.
Por isso, não estamos muito interessados no gráfico acima, pois ele não considera os erros. Estamos interessados no gráfico de N, que nos dá de fato o impacto na nota ao responder os n itens:
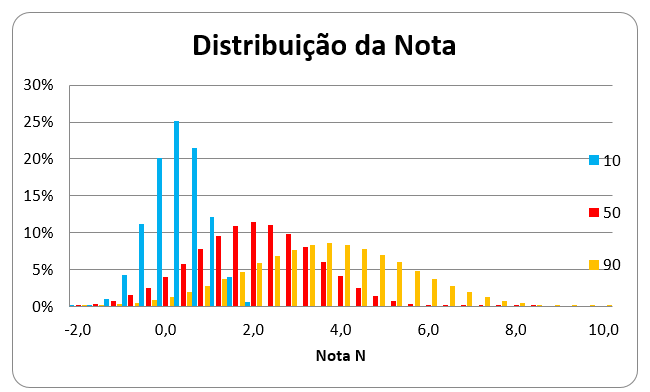
Esse gráfico é bem interessante de analisar. Quando respondemos muitos itens sem ter certeza, é claro que há uma chance de errarmos muitos itens e ter uma nota muito negativa. As distribuições acima mostram que, apesar de ser possível disso ocorrer, a probabilidade é extremamente pequena.
Por exemplo, é possível responder os 90 itens e errar todos, dando um impacto de -90.0,2=-18 pontos na nota? Sim, mas a probabilidade disso ocorrer é de
0,0000000000000000000000000000000002%.
É por isso que no gráfico nem aparecem probabilidades para N<-2, elas são muito baixas.
Mas ok, o impacto na nota não precisa chegar a -18 pontos para ser considerado ruim. Ter uma probabilidade relevante de ter um N de -1 ou -2 já é bastante prejudicial. A tabela abaixo mostra algumas probabilidades de notas baixas ocorrerem para alguns cenários:

O que essa tabela nos mostra? Que, mesmo respondendo muitos itens sem 100% de certeza, a probabilidade de obter uma nota muito negativa (perder mais de 2 pontos) é muito pequena.
Claro que perder 1 ponto inteiro ou mais na Anpec já é bastante ruim. Mas o que a tabela nos mostra também é que a probabilidade disso ocorrer começa até a diminuir a partir de certa quantidade de itens respondidos. Isso ocorre porque a distribuição se desloca para a direita (maior valor esperado) quando aumentamos a quantidade de itens respondidos.
Vimos então que, considerando os riscos de ter uma nota muito negativa, pode fazer sentido responder mais itens sem tanta certeza assim. Agora vamos ver o quanto responder esses itens pode beneficiar a nota, e com qual probabilidade:

Em termos de benefícios, fica claro que vale a pena responder os itens SE soubermos que temos uma probabilidade maior do que 60% de acerto (essa condição é bastante importante!).
Considerações Finais
Quantidade de Itens
Nesse artigo, consideramos alguns cenários diferentes de quantidades de itens respondidos sem certeza, o parâmetro n.
No entanto, como para ser bem classificado na Anpec o que importa é sua nota geral, essa quantidade de itens deve levar em consideração o total de todas as provas (pelo menos daquelas que tem peso para o seu interesse). É por isso que pode fazer sentido pensarmos em valores de n mais elevados, como n=100.
Isso atrapalha um pouco nossa análise para ser aplicada na prática. Imagine que você está fazendo a primeira prova da Anpec, a de Macroeconomia. Você vai ter que decidir se responde ou não alguns itens que não tem certeza da resposta, sem saber da quantidade total de itens que não terá certeza durante o exame todo, inviabilizando ter em mente algumas probabilidades aqui calculadas.
Probabilidade de Acerto
Durante esse texto, analisamos se vale a pena responder itens cuja probabilidade de acerto era de 60%. Fizemos apenas um exercício com essa premissa. Na realidade, no entanto, essa probabilidade não é observável, além de não ser constante para todos os itens.
Você, ao decidir responder ou não um item da Anpec, infelizmente não saberá sua probabilidade de acerto. Você pode intuir seu grau de confiança subjetiva, mas isso está longe de ser a probabilidade de responder a questão corretamente.
Mais grave do que isso: numa prova de “Verdadeiro” ou “Falso” como é a Anpec, é comum os elaboradores das questões tentarem induzir o candidato ao erro. Dessa forma, às vezes o candidato que sabe pouco do assunto pode ter mais de 50% de errar, por “cair na armadilha” da questão. Ou seja, às vezes saber pouco é pior do que não ter noção!
O que fazer então? Treine fazendo provas de anos anteriores! Marque as questões em que você ficou na dúvida se responderia ou não e analise se seria bom ter respondido elas. Assim você vai aprendendo se anda respondendo itens de mais ou de menos.
Um pouco de Economia Comportamental…
Suponha que tem dois itens em que você sabe mais ou menos a resposta, mas está na dúvida se responde os dois ou nenhum. Considere que você acabou optando por responder os dois, e acabou acertando um e errando o outro. Qual o impacto na sua nota? Zero. Mas você vai ficar ok com isso? Provavelmente não.
Em termos de sentimento, provavelmente você dará mais peso para o item que você errou do que para o que você acertou, gerando uma sensação de que não valia a pena responder os itens sem ter certeza (mesmo que, no fim das contas, o resultado teria sido o mesmo se não tivesse respondido nenhum dos itens). Esse é um fenômeno bem conhecido, estudado na área de Economia Comportamental.
Mais do que isso, olhando o item que você acertou, você pode até começar a achar que realmente sabia a resposta dele desde o começo, não o considerando como um “ponto positivo” por ter respondido itens sem ter certeza.
Como, no fim das contas, o que importa para Anpec é sua nota final, tem que tomar cuidado com sentimentos que não fazem sentido e podem fazer com que você responda menos itens do que deveria.
O que fazer então? O mesmo que sugerimos antes: Treine fazendo provas de anos anteriores! Marque as questões em que você ficou na dúvida se responderia ou não e analise se seria bom ter respondido elas. Esse método vai te mostrar uma avaliação objetiva sobre se você está respondendo questões de mais ou de menos.
Para algumas pessoas pode até ser interessante ir além: analisar sua métrica de certeza subjetiva. O que seria isso? Ao fazer questões de anos anteriores, treine escrever ao lado do item o percentual de certeza que você tem sobre a resposta que está dando. Ao corrigir as questões você poderá, ao longo do tempo, entender a partir de qual valor de certeza geralmente vale a pena responder, usando isso no dia da prova.

Variância na nota pode ser bom?
Nesse artigo, vimos dois lados de responder questões sem ter certeza da resposta: isso faz com que o valor esperado da nota aumente, mas também aumenta sua variância.
Aumentar valor esperado da nota certamente é algo positivo, mas e aumentar a variância? Tratamos como se fosse algo ruim, como se não quiséssemos correr o risco de perder muita nota ao decidir responder itens sem muita certeza.
Por outro lado, aumentar a variância pode ser algo positivo, pois pode fazer com que sua nota aumente! Imagine que você tenha a sorte de acertar a grande maioria dos itens que você não sabia direito!
Quando a variância certamente é ruim? Suponha que você esteja muito bem preparado para a Anpec, de forma que está seguro que garante sua aprovação só respondendo os itens que tem muita certeza. Nesse caso, pode não fazer muito sentido correr riscos ao responder itens que não sabe direito.
Quando a variância certamente é boa? Na situação contrária. Você sabe que depender somente do que você sabe com bastante certeza não será o suficiente para sua uma boa colocação. Então é melhor começar a responder mais perguntas. Nesse caso, tanto o valor esperado quanto a variância na nota apontam na direção de responder mais!
Conclusão
Esse artigo não está, de maneira alguma, incentivando você a sair respondendo todas as questões da Anpec sem critério algum!
Além de aplicar o conteúdo da prova de Estatística cobrado pela Anpec, a ideia aqui era mostrar que também há pontos positivos em responder questões mesmo sem ter certeza absoluta de suas respostas.
O quanto responder, isso é algo que você tem que descobrir principalmente utilizando provas anteriores para teste.
Se você está indo para a Anpec desse ano sem ter feito esse treino, tudo bem. Lembre-se deste artigo na prova e pondere com cuidado sua incerteza nas questões. Primeiro responda tudo que você tem certeza e depois volte analisando os itens deixados em branco. Mostramos que pode valer a pena responder alguns itens sem certeza absoluta da resposta.
Este artigo foi escrito por Douglas Bokliang.
