Preliminares
A função f não foi completamente definida, mas sabemos que seu domínio coincide com sua imagem, ambos são [0;1].
O conjunto A são os números x entre 0 e 1 tal que f(x)=x.
Para resolvermos os itens vamos sempre pensar nas curvas de x e de f(x). O conjunto A conterá os valores do eixo x em que as duas curvas se interceptarem, ou seja, f(x)=x. Apesar de não sabermos como é a função f exatamente, sempre temos que lembrar que sua imagem deve ser o conjunto [0;1].
Vamos sempre tentar ver se é possível cada sentença ser falsa. Encontrando apenas um contraexemplo em que isso ocorre, a afirmativa torna-se falsa.
0-Falso
Vamos tentar ver se A pode ser vazio, ou seja, se pode não haver intersecção entre o gráfico de x e o gráfico de f.
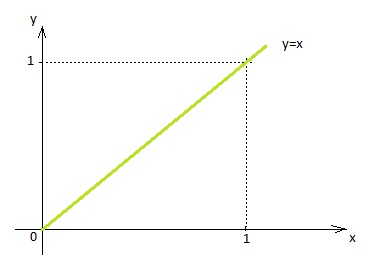
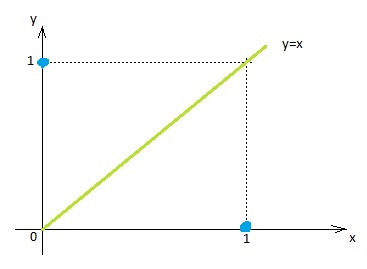
Para isso, vamos iniciar com o gráfico de x abaixo:
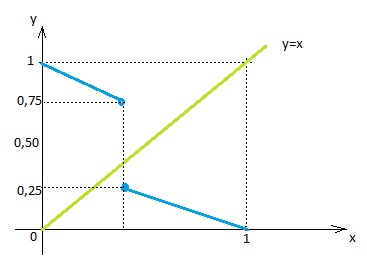
É possível desenharmos uma função f que tenha como imagem [0;1] e que não cruze com o gráfico acima? Vamos tentar:
O gráfico de f acima não cruza com o gráfico de x. No entanto, sua imagem não é [0;1] pois nenhum valor “chega” entre 0,25 e 0,75.
Mas podemos alterar a função acima para que ela atinja todos os valores entre [0;1]:
Logo, existe função f, como acima, que não tem intersecção com o gráfico de x. Assim, pode não haver nenhum x tal que f(x)=x e A ser vazio.
1-Falso
Se f é contínua, f não pode ser como no gráfico anterior, temos que desenhar f “sem tirar o lápis do papel”.
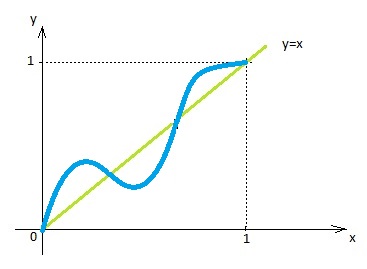
Aqui a pergunta é: será que f pode interceptar o gráfico de x em mais de um ponto, fazendo com que A tenha mais de um elemento? É simples desenhar um gráfico contínuo em que isso ocorre, por exemplo:
Logo, A não é necessariamente unitário.
2-Verdadeiro
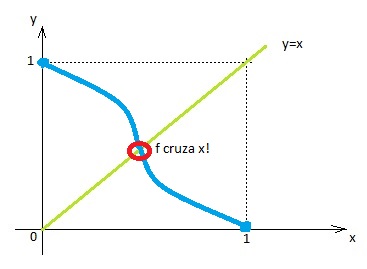
Agora temos a condição inicial de que o gráfico de f se inicia com y=1 e termina com y=0:
É possível ligarmos os pontos (0;1) e (1;0), “sem tirar o lápis do papel” e sem cruzar a curva de x? Sempre lembrando que, para f ser uma função, não pode haver dois valores de diferentes de f para um mesmo valor de x.
O gráfico de x funciona como uma barreira bloqueando completamente o caminho entre os dois pontos. Você não irá conseguir ligar os dois pontos sem cruzar essa barreira, pode tentar à vontade! =)
Dessa forma, a curva de f vai ter que cruzar o gráfico de x para ligar os pontos (0;1) e (1;0). Nesse ponto de intersecção, o valor de x vai pertencer a A, fazendo com que A seja diferente de vazio.
3-Falso
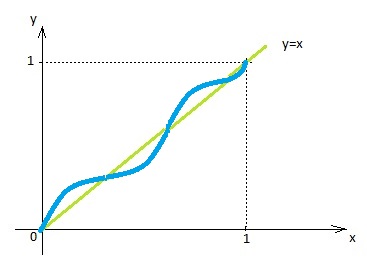
Aqui, f é estritamente crescente. Para que a imagem de f seja [0;1], f deve iniciar em 0 e terminar em 1 (se iniciar em um valor maior que zero, não poderá depois baixar seu valor para zero).
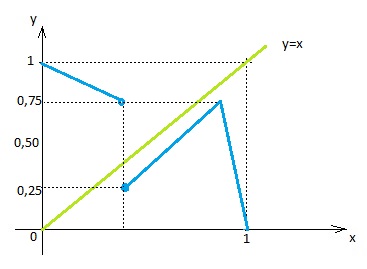
É possível haver mais de um cruzamento com a curva de x, sendo que f sempre aumenta? O gráfico abaixo mostra que sim:
Podemos ir alterando a inclinação de f para que ele cruze quantas vezes quisermos o gráfico de x. Logo, A pode ter mais de um elemento.
4-Falso
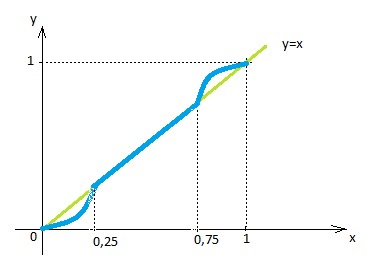
É possível que A tenha infinitos elementos? Para que isso ocorra, basta que f tenha um segmento em comum com a função y=x:
No gráfico acima, há infinitos valores entre 0,25 e 0,75, e todos tem f(x)=x. Logo, A=[0,25;0,75] possui infinitos elementos (lembre-se que entre dois números reais existem outros infinitos números reais).