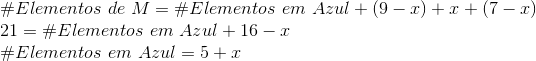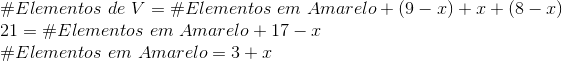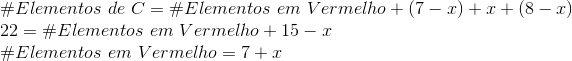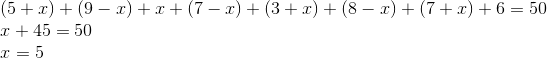Preliminares
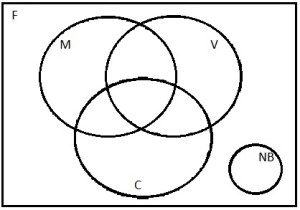
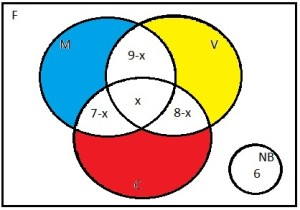
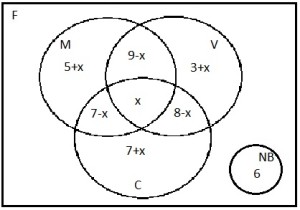
Para resolver esta questão, vamos considerar a figura abaixo:
Onde:
–F representa todos os participantes da festa
–NB representa aqueles que não bebem bebida alcoólica
–V representa aqueles que bebem vodka
–M representa aqueles que bebem Martini
–C representa aqueles que bebem cerveja
Perceba que pode haver intersecção entre V, M e C, já que um participante pode beber mais de um tipo de bebida.
A ideia da solução é tentar preencher os conjuntos com a quantidade de elementos em cada região.
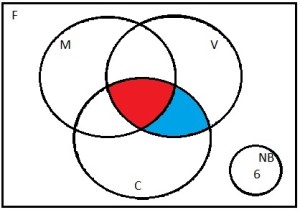
De cara, não conseguimos preencher muita coisa, somente o conjunto NB. Isso porque apesar de sabermos, por exemplo, que 8 bebem vodka e cerveja, não sabemos quantos desses bebem também martini:
Sabemos que a região vermelha e a região azul possuem juntas 8 elementos, mas como preencher cada região separadamente?
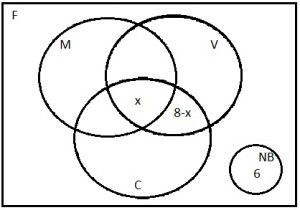
Como ainda não conseguimos separar essas quantidades, vamos dizer que a região vermelha possui x elementos (logo, a azul possui 8-x):
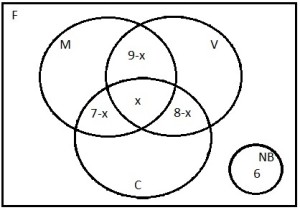
Da mesma forma, fazendo somar 7 na intersecção de M e C e 9 na intersecção de V e M:
Agora o próximo passo é preencher as regiões com participantes que só bebem um tipo de bebida, coloridos na figura abaixo:
Vamos calcular as quantidades das partes coloridas, começando por M:
Agora V:
Agora C:
A figura fica dessa forma:
Agora podemos encontrar o x somando todas as quantidades acima e igualando à quantidade total de participantes da festa (50):
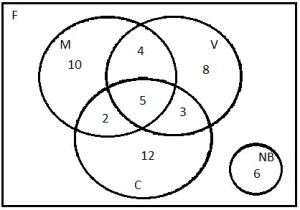
E, substituindo x, temos a figura final:
Agora fica fácil respondermos as perguntas:
0-Verdadeiro
Direto da figura acima.
1-Verdadeiro
Direto da figura acima.
2-Falso
Pela figura acima, são 12.
3-Falso
Pela figura acima, o total de participantes que bebem martini é 10+4+5+2=24, logo 50-24=26 não bebem martini.
4-Verdadeiro
Pela figura acima, 10+4+8=22 bebem alguma bebida, mas não cerveja.