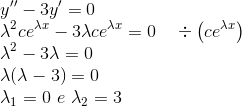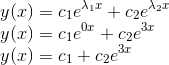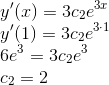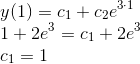Resolução
A solução para uma equação ordinária homogênea é do tipo:
Calculando as derivadas de primeira e segunda ordem:
Substituindo na equação:
Como tem dois valores possíveis para λ, a solução fica:
Para determinar c1 e c2, temos que usar as condições de contorno:
E:
Assim, a solução geral é:
E a primeira derivada:
No ponto x=0:
Resposta: 06