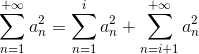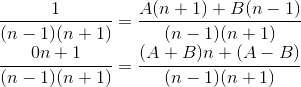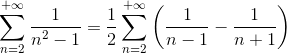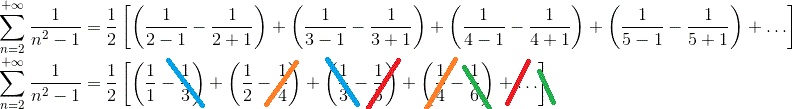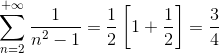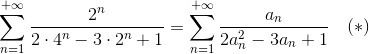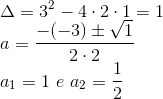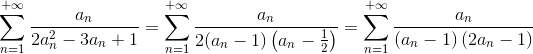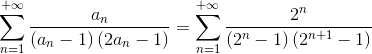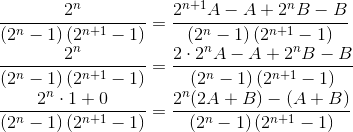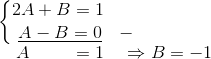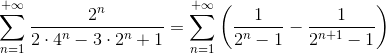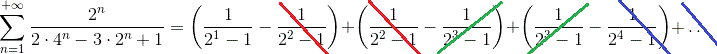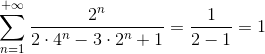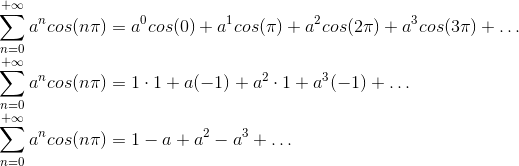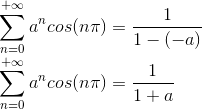0-Verdadeiro
Como a e r são fixos, quando nà+∞, a/nà0, (1+ a/n)à1 e (1+ a/n)rà1. Ou seja, a sequência converge para 1 não importa o a e r, desde que fixados.
1- Verdadeiro
Se converge, anà0.
Então, a partir de algum termo da soma, a sequência tem que ter apenas elementos menores do que 1. Seja i a posição do último termo tal que ai>=1.
Assim, para todos os termos que vem depois de i, o termo ao quadrado é menor do que o próprio termo:
Isso porque um número menor do que 1 ao quadrado é menor do que o próprio número.
Assim, a série converge pois ela é menor do que , sendo que esta converge.
Veja que:
Como tem número limitado de termos, ela não pode divergir.
Então, as duas parcelas convergem e a série também.
2-Falso
Como dá para fatorar o denominador, vamos tentar separar cada termo da sequência em uma soma:
Quem tem mais prática pode perceber que A=1/2 e B=-1/2 satisfaz acima.
De qualquer forma, vamos mostrar como determinar A e B:
Comparando os numeradores da última igualdade, vemos que:
Assim:
Substituindo na série:
Vamos “abrir” a série, apenas para visualizar o que acontece:
Perceba que todos os termos negativos são cancelados pelo termo positivo equivalente, o qual se encontra sempre 3 posições depois. Assim, quase tudo se zera, restando:
3- Verdadeiro
Achei esse item um tanto complicado…
Para facilitar um pouco, vamos considerar uma sequência auxiliar {an}n≥1 tal que an=2n:
Agora vamos tentar fazer algo parecido com que fizemos no item passado. Fatorando o denominador:
Sendo a1 e a2 as raízes do polinômio 2a2-3a+1:
Voltando para (*):
Substituindo an=2n:
Assim como no item anterior, vamos tentar “quebrar” o termo da série em duas frações, da seguinte forma:
Com mais prática, é possível notar que A=1 e B=-1 satisfaz a identidade acima.
De qualquer forma, desenvolvendo para encontrar o A e B:
Assim, A e B devem satisfazer:
Então, voltando para a série:
“Abrindo” essa soma para visualizar o que acontece:
Veja que cada parcela negativa é cancelada pela parcela seguinte, restando apenas a primeira parcela. Assim:
4-Falso
Vamos “abrir” o somatório:
Perceba que é uma soma de PG com razão a. Como 0<a<1, ela converge para o seguinte: