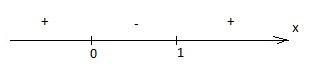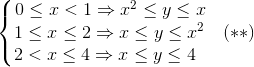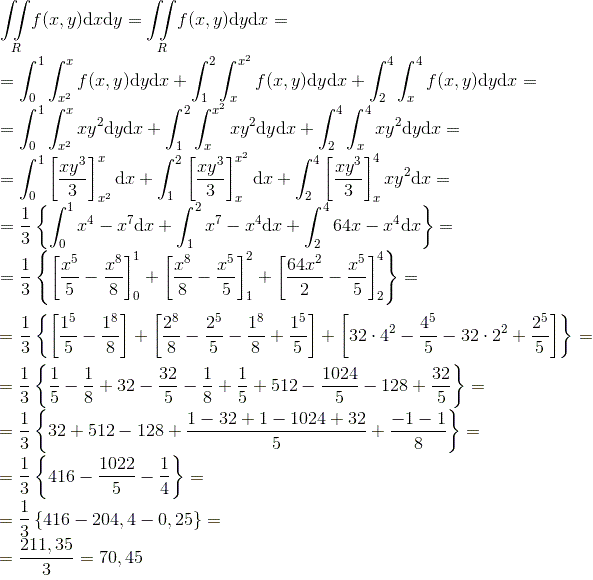Resolução
A parte mais complicada dessa questão é estabelecer os limites de integração.
Enquanto x varia de 0 a 4, y varia do menor entre x e x2 ao maior entre esses dois valores, desde que entre 0 e 4.
Para iniciar, vamos ver quando x é maior do que x2:
x é maior do que x2 quando x(x-1)<0. Nos pontos x=0 e x=1, x(x-1) troca de sinal. Como x(x-1) é positivo quando x é maior do que 1, veja o sinal de x(x-1) em função de x:
Como x é maior do que x2 quando x(x-1) é negativo, então isso ocorre quando x está entre 0 e 1.
Assim:
Veja que (*) deve também satisfazer a condição do domínio de y: y≤4. Para isso:
Como x é não negativo, podemos ignorar o módulo.
Assim, quando x é maior do que 2, y não pode variar de x até x2, pode ir somente até 4. Dessa forma, os limites da região R são:
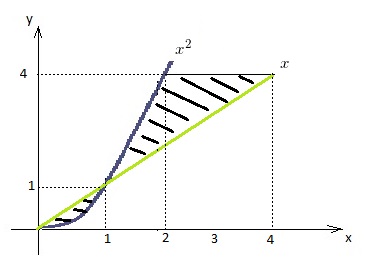
Apenas para ficar mais fácil de visualizar, R corresponde à área hachurada abaixo:
Agora podemos ir para o cálculo da integral, separando ela nas 3 regiões, conforme (**):
Resposta: 70
Comentário
Considero a primeira parte dessa questão, de determinar a região R, muito boa. No entanto, a partir daí vem muita conta, o que dificulta muito a resolução do exercício já que o tempo na prova da Anpec é muito escasso. Fazer essa questão podia “roubar” um tempo precioso das demais, correndo ainda um sério risco de errar uma conta no meio do caminho. Acho que poderiam ter utilizado uma função f mais simples para diminuir esse problema.