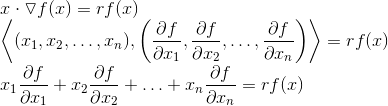Mat 2016 – Questão 9

Preliminares

Esta é uma questão sobre o Teorema de Euler, que, sendo bem breve, nos diz que, sendo f uma função homogênea de grau r:

Sendo:

Além disso, todas suas derivadas parciais são homogêneas de grau r-1.

0-Verdadeiro

Apenas para ficar claro, o gradiente de f é o seguinte:

Ou seja, cada componente do gradiente de f é uma derivada parcial de f.

Sendo f homogênea de grau r, cada componente do gradiente é homogêneo de grau r-1 pelo Teorema de Euler.

1-Verdadeiro

O enunciado apenas utilizou uma notação mais compacta, utilizando um produto escalar. Vamos destrinchar ele:

Veja que essa é justamente a fórmula de (*).

Se uma função satisfaz (*) para todo x do domínio, quer dizer que ela é homogênea de grau r.

2-Falso

O problema aqui é quando são duas funções homogêneas de graus diferentes, por exemplo:

f é homogênea de grau 1 e g é homogênea de grau 2, já que:

Seja a função h(x)=f(x)+g(x):

h não é homogênea, pois:

Ou seja, não conseguimos colocar na forma:

3-Falso

Essa é uma daquelas questões em que levamos um tempo somente para entender o enunciado…

1º modo

Assim como nesse item, algumas vezes podemos pegar “emprestado” nosso conhecimento de micro para resolver uma questão de matemática.

Isso pode ser útil por dois motivos: podemos pegar resultados conhecidos de micro e facilita a compreensão do problema, já que estamos dando um significado às fórmulas matemáticas.

Aqui nessa questão, o próprio formulador usou notação usual de micro para nos dar essa dica: c(q) é a função custo, dada a quantidade q produzida; f(x) é a função de produção, dados os insumos x; w_i é o preço (fixo) do insumo x_i.

A função custo c(q), escrita matematicamente como no enunciado, apenas significa que c(q) é o custo mínimo para produzir q.

Pergunta: o que acontece com a função custo quando duplico a quantidade produzida? c(2q)=?

Se r>1, temos que a produção apresenta ganho de escala. Ou seja, produz mais do que o dobro quando duplicamos os insumos dela. Outra forma de pensar é: precisa gastar menos do que o dobro para produzir o dobro: c(2q)<2c(q).

Assim, se r>1, a função custo não é homogênea de grau r. Se for homogênea (não mostramos se é ou não), é de um grau menor do que 1, já que c(2q)<2c(q) e, para ser homogênea de grau 1, teria que ter c(2q)=2c(q). Logo, o item é falso.

Um raciocínio análogo pode ser usado para r<1.

2º modo

Agora vamos resolver fingindo que não sabemos nada de micro.

Vamos calcular c(q):

Vamos supor que x₀ é o x que minimiza wx tal que f(x)=q:

Agora vamos calcular c(λq):

Como f é homogênea de grau r, fazendo x=αx₀:

Substituindo em (*):

Ou seja, quando multiplicamos q por λ, o valor de x é multiplicado por α=λ^1/r≠r (de x₀ vai para αx₀) e, consequentemente, wx também é multiplicado por α=λ^1/r≠r, já que w é fixo:

Da equação anterior, notamos que c é homogênea de grau 1/r.

4-Verdadeiro

Do Teorema de Euler:

Dividindo os dois lados da igualdade por f(x):

Elasticidade de y em relação a x_i é:

Substituindo em (**):