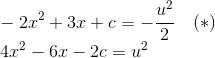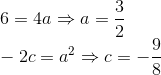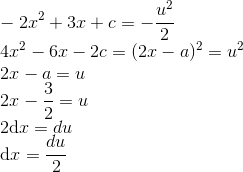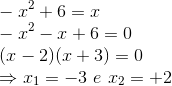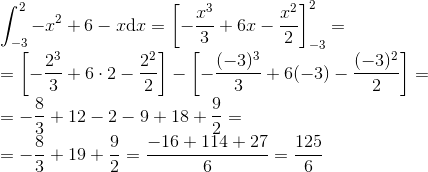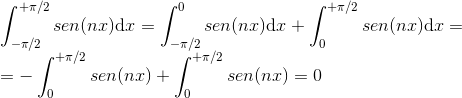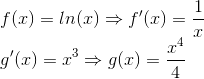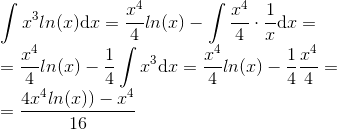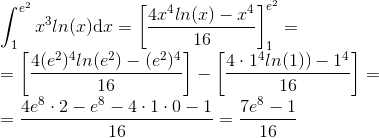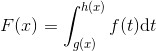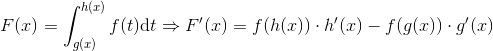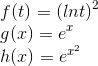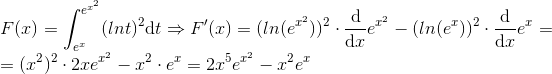Mat 2016 – Questão 7

0-Falso

Como o enunciado nos deu uma primeira integral como exemplo, vamos tentar ajustar a segunda para que ela fique no mesmo formato. Para isso, vamos multiplicar e dividir por uma constante para ver o que ocorre:

Ok, não ajudou muito… mas se a constante fosse da forma e^c…

Agora isso pode nos ajudar. Se escolhermos apropriadamente a constante c, podemos deixar a segunda integral na forma da primeira. Para isso, o expoente do e deve ser da forma ­-u²/2:

Assim, c deve ser tal que 4x²-6x-2c seja um quadrado perfeito. Para isso, deve ser da forma (2x-a)²:

Comparando os dois lados da identidade:

De (*), a segunda integral virou:

Com:

Substituindo em (**):

Essa integral é idêntica à primeira, logo temos seu resultado:

1-Verdadeiro

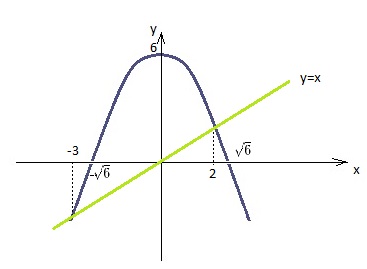
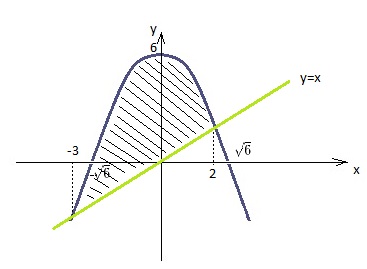
Vale a pena fazer um esboço do gráfico com os principais pontos:

Note que:

-a parábola corta o eixo x quando:

-a parábola corta o eixo y quando:

-a parábola cruza a reta quando:

Queremos calcular a seguinte área:

Para isso, basta integrar (-x²+6)-x entre -3 e 2:

2-Falso

A função sen(nx) é uma função ímpar, já que sen(nx)=-sen(-nx).

Lembre-se que a integral calcula a área entre acima do eixo x e o gráfico da função; nesse caso, a área abaixo do gráfico no trecho entre –π/2 e 0 acaba “cancelando” a área acima do trecho entre 0 e π/2, resultando num valor total igual a zero.

De uma forma mais algébrica: a integral calculada de –π/2 a 0 é igual a integral calculada de 0 a π/2, apenas com sinal trocado. Logo, quando calculamos a integral de –π/2 a π/2, o valor encontrado será 0:

3- Verdadeiro

A parte que está dificultando a integração é o ln(x), o trabalho seria fácil se só tivesse o termo polinomial. Assim, vamos “sumir” com o ln(x) utilizando integração por partes.

Na integração por partes, dividimos a função que estamos integrando como produto de duas, f(x) e g’(x), sendo que conseguiremos calcular a integral em função da integral do produto de f’(x) e g(x):

Queremos que ln(x) seja f(x) ou g’(x)? Vamos fazer f(x)=ln(x) para que a integral do lado direito da equação acima use a derivada de ln(x), 1/x, facilitando as contas:

Substituindo e fazendo as contas:

Utilizando os limites de integração:

4- Verdadeiro

Para resolver essa questão, teremos que utilizar o Teorema Fundamental do Cálculo.

Numa situação mais simples, o Teorema Fundamental do Cálculo nos diz que:

Note que o limite inferior da integral é uma constante ‘a’ e o limite superior é ‘x’.

Na situação da afirmativa, isso não ocorre, temos uma integral da seguinte forma:

Ou seja, temos funções de x nos limites da integral.

Podemos usar a forma mais geral do Teorema Fundamental do Cálculo para resolver a derivada desse tipo de integral:

Onde, de acordo com a sentença:

Substituindo:

Fazendo x=2: