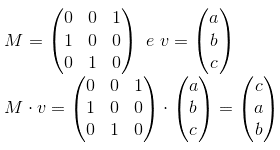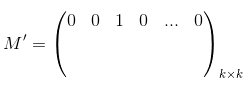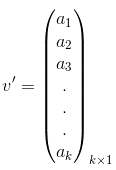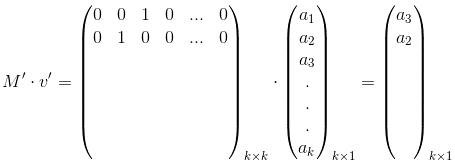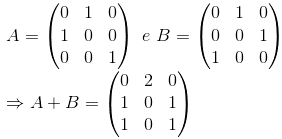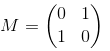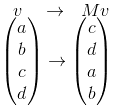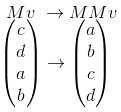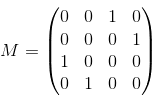Mat 2016 – Questão 4

Preliminares

Acho que vale a pena primeiro entender melhor o que ocorre quando multiplicamos uma matriz de permutação e um vetor.

Considere a matriz de permutação M e o vetor v:

Perceba que o produto M.v forma um vetor com os mesmos elementos de v, mas em ordem trocada. Não é à toa do nome matriz de permutação para M!

Esse foi apenas um exemplo, mas para entender que isso sempre ocorre, vamos considerar outra matriz de permutação M’, esta com dimensão k.

Na primeira linha, deve haver apenas um número 1. Digamos que o número 1 se encontra na 3ª coluna:

Por enquanto, não se preocupe com as demais linhas.

Agora, seja o vetor v’ com k elementos:

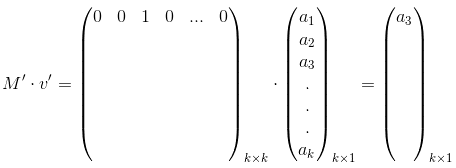
Quando multiplicamos M’ por v’, encontraremos um vetor cujo primeiro elemento será a₃:

Isso porque o número 1 da primeira linha de M’ está na 3ª coluna.

Da mesma forma, se o número 1 da segunda linha de M’ estiver na 2ª coluna, a₂ que estará na segunda linha de M’.v’:

E isso acontece para todas as linhas de M’. Como tem apenas um número 1 em cada coluna, todos os valores de v’ vão aparecer em M’.v’, com a única diferença que podem estar em posição trocada.

Agora que entendemos o que uma matriz de permutação faz, vamos às questões.

0-Falso

Como uma matriz de permutação possui apenas um número 1 em cada linha e em cada coluna, a soma de duas matrizes de permutação vai ter, em cada linha e em cada coluna, dois números 1’s ou um número 2, de forma que não será de permutação.

Por exemplo, sejam as matrizes de permutação A e B:

1-Verdadeiro

Seja M1 e M2 duas matrizes de permutação nxn e v um vetor nx1.

M1.v=v1, sendo que v1 tem os elementos de v permutados.

M2.v1=v2, sendo que v2 tem os elementos de v1 permutados, ou, da mesma forma, os elementos de v permutados.

Seja M=M2.M1:

Ou seja, M é uma matriz de permutação, uma vez que sua multiplicação por v gerou v₂, um vetor permutado de v.

Como M é um produto de matrizes de permutação, podemos afirmar que o produto de matrizes de permutação gera uma matriz de permutação.

2-Verdadeiro

Como explicado anteriormente, Mv gera um vetor com os mesmos elementos de v, apenas com posições trocadas. Dessa forma, Mv tem a mesma norma que v.

3-Verdadeiro

S contém os vetores de R^nx1 cuja soma dos elementos é igual a 1.

Como M é uma matriz de permutação, a transformação T(v)=Mv apenas permuta os elementos de v.

Dessa forma, se v pertence a S, Mv também pertence, já que a soma dos elementos de Mv é igual à soma dos elementos de v.

Assim, podemos dizer que aplicando T a qualquer elemento de S, teremos um elemento de S, então T(S) está contido em S.

4- Falso

Se M é uma matriz de permutação, então M² também é (conforme item 1).

Se M²=I, não necessariamente M=I. Um exemplo simples é:

M inverte a posição dos 2 elementos de vetores 2×1.

Note que M²=I sendo que M≠I. Para isso, basta fazer a conta ou perceber que se invertermos a posição dos elementos de um vetor 2×1 e depois invertermos novamente, chegaremos ao vetor original.

Um exemplo um pouco mais complicado segue abaixo.

Se a permutação aplicada for tal que ocorra o seguinte com o vetor v:

Ou seja, os elementos “rolam” duas posições pra baixo, sendo que se estiverem na 4ª linha, voltam para a 1ª.

Se aplicarmos novamente a mesma transformação:

Note que aplicamos a permutação duas vezes, ou seja, multiplicamos v por M² e chegamos ao próprio v. Logo, M²=I sendo que M≠I.

Apenas por curiosidade, a matriz M do caso acima é: